• In recent months, two words are very much familiar with every citizen of the world, “COVID-19” and “Pandemic”. Across the globe, we are fighting with this invisible powerful virus without any medicine but LOCKDOWN.

• Background: As per the report of WORLD HEALTH ORGANIZATION, on 7 January 2020 in the case of Wuhan in China, the first Novel Coronavirus was identified. It was named severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) by the International Committee on Taxonomy of Viruses on 11 February 2020.

• World Scenario: At present in the world, huge number of cases are there with several deaths recovered cases. Until now there are large numbers of active cases including mild and serious cases, there are active cases and closed cases (including deaths and recovered) also.

• Scenario in India: INDIA is also very much affected in COVID-19 which is increasing day by day. The following 6 diagrams may help us to understand the nature of growth of COVID-19 in India and its various angles.

• Role of Mathematics in COVID-19: Now the question is how mathematics can help in this regard. Firstly, let us look into the following diagram,

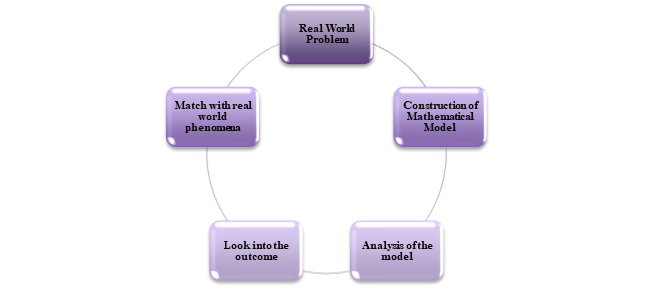
CYCLE OF A MATHEMATICAL MODEL

At present, every disease can be converted to mathematics using Mathematical Modelling. A modelling is a process to convert a real life problem into a mathematical phenomenon using its’ logic. The cycle can be understood from the above diagram.

We need few parameters to form a mathematical model based on a real life situation. Regarding COVID-19, also people are working on various model but until now as the situation is not very much clear, so no such well-established model has come up.

Model parameters and its importance in COVID-19:

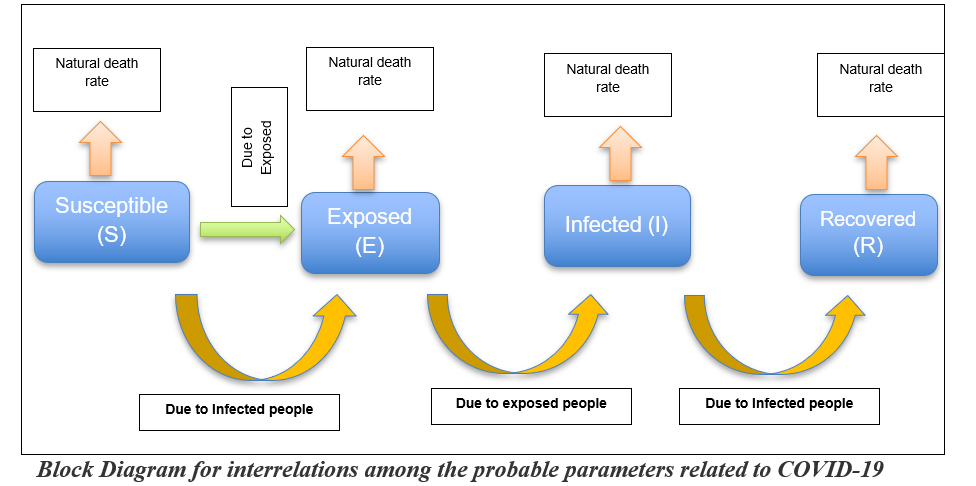
The following probable parameters can be considered for forming a model regarding this disease.

1. Susceptible (S) – who are affected by others
2. Exposed (E)- who are not showing any symptoms but able to infect others.
3. Infected(I)- who have fully developed symptoms and can easily infect others.
4. Recovered (R)- who recovered normally or by some other medicines.

As soon as some drugs will be available in the market, that also can be taken into consideration to make the model more realistic. This kind of model may be applicable in India where various transmission dynamics will be considered. We can visualize the interrelation among these parameters as follows:

What is the Goal of this type of model?

Here after successfully forming the model, we can study its stability analysis of the model both locally and globally. In addition, we try to find the Basic Reproductive Number – which describes the expected number of cases directly generated by one case of the population where all individuals are susceptible to infection. Based on this number we can generate conditions by which the model can be stable or asymptotically stable or unstable.

Also based on  we can also predict the risk factor to the society due to this invisible virus effect. At present, there are no drugs for this virus. As soon as some drugs will be there, then drug parameter may be incorporated in the model to make the model more realistic. Based on the drug, Reproduction number will change and then the scenario will be changing.

Limitations of the model:

As there are various significant biological factors, which may not be included in the model as solving a non-linear mathematical model may be very much time consuming and complex. Therefore, for simplifying we may linearize some of the factors, which will deviate the model from its original shape.  Hence, a model will always help us to understand this overall scenario but not the particular one.