Now a days data analysis becomes an integral part of our social life. Collection of data is the basic need to analyze data. In some particular scenario those collected data increases rapidly. In such cases we have to tame the increase of data.

What is Data Explosion?

The word explosion usually not sounds to be pleasant for us. This word always reminds us the history of Hiroshima and Nagasaki atomic explosion. As we know history repeats itself, in this modern era we are also in a war and the war is the war of data collection. In every aspects of our life like Science and Engineering, Commerce etc, we are collecting and storing data at an ever-increasing rate. This rapid increase of data creates an abundance.

Challenge to Overcome: 

To overcome from this adverse situation becomes a challenge for us. Many mathematicians and statisticians are working on this. Every time they are trying to find some new aspects to deal with.

Can Topology Help?

Being major branch of Mathematics, Topology has a deep impact on study of set theoretical and geometrical aspects of mathematics. One hardly can think to employ Topology for preventing this data explosion. But in the last fifteen years, there has a surge of interest and activity to apply Topology in developing Topological Data Analysis (TDA). This TDA yields not only the practical tools for studying data but also some pleasant mathematical surprises. This TDA has several applications in the area of Science and Engineering, Oncology, Neuroscience and Biophysics.

Basic Goal of TDA:

The basic goal of TDA is to develop tools for studying geometric features of data by means of Topology. Here we need to consider data as a finite set of points in a space. In general, the space in which our points lie can have many dimensions but we may think that those points are in two or three dimension. We can also consider them as a hyperspace generalization . For an example each point in the data set in 3D corresponds to a cancerous tumor and the co-ordinates x, y and z corresponds to the level of expression of different gene in a tissue sample of the tumor.

Use of Topology to study geometric features of Data:

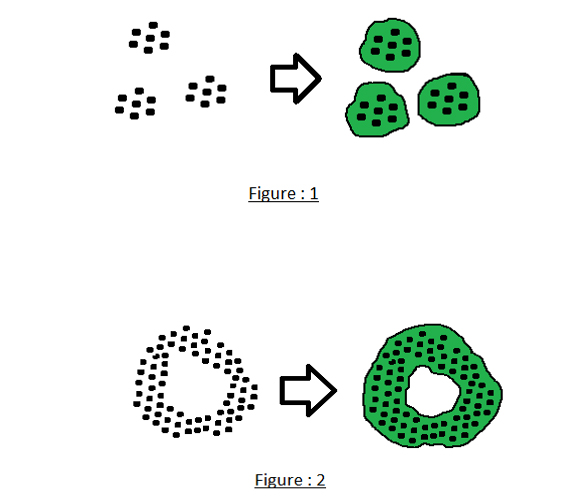
Here we are going to discuss topological significance to study geometric properties of data briefly. Topology always offers tools to compute number of holes and component in geometric objects. We are going to apply this tool in our study of data. For that let us take a data set  of  points in a space which has  components and no holes. We are going to study  using Topology. But the topological properties of  can’t be used directly, rather those are used as  ‘metric’ or  ‘distance’ Topology. This is also called  ‘thickening’ property of .

For an example we have given two diagrams below: