Most of the physical systems of nature are not regular geometric shapes of standard geometry derived from Euclid. Most of the shapes we deal with Euclidean or classical geometry are smooth shapes like circles, triangle, rectangular volume, spheres, arc, cylinder, lines, planes etc and are classified to have integer dimensions 1, 2 or 3. A line is one dimensional because we need only one number to uniquely define any point on it. This number may be the distance from any point. This also includes curve, boundary etc. In surface we need two numbers to specify any point on it and for volume it is three numbers. Concept of dimension is basically described by two ways. The number of co-ordinates we need to describe the system or number of dynamical variables needed to specify the system. But the fact is that the natural objects we see around us are strikingly different. Randomness is natural ingredients of most Natural phenomena. A different geometry is needed to describe them. Concept of dimensions seems to be different in such systems. ‘Clouds are not sphere, mountains are not cone, coast lines are not circles, bark is not smooth nor does the lightening travel in straight line’. How dimension can be defined to describe such systems? B. Mandelbrot gave a deeper thought into it.
How long is Coast of Norway?
This is the most interesting question asked about the length of the coast of Norway. If we go for a straight cut answer it will be it depends how closely you look at it or how long your measuring stick is.

Fig-1 –Coast of Norway
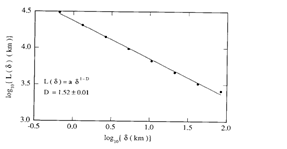
Fig-2- Measured length in log-log plot
In Fig-1 the deep fjords in western coast of Norway is shown clearly. If one takes the map and measure with a ruler one can get certain value but if one opt for walking along the coast and measure the steps, one will arrive at a very different and larger value of the perimeter. While passing one could walk a divider with steps ‘δ’ km each along the coast line on the map and count the number of steps. If N (δ) number of steps are needed to move from one end to other in the map, the estimated length will be L (δ) = N(δ).δ. Every time we increase the resolution δ, we will observe increase in the measure of length of the coastline. Fig-2 shows the measured length L (δ) as function of size δ of the δ x δ square to cover the coastline on the map and shows that the coastline does not have any fixed value of length as we reduce the yardstick length δ. It is interesting to observe the curve fitted well with the expression L (δ ) = A. δ1-D with D ~1.52. For ordinary curve the ‘A’ should be equal to total length i.e. for sufficiently small δ exponent D equals to1 but here it is 1.52.The coast line curve is a Fractal with fractal Dimension 1.52. Fractal dimensions are usually non-integers.
Fractal Dimension: Koch Curve:
Once we leave the secure ground of conventional geometry a whole zoo of fractal dimension appears! The fractals are defined in several ways. It is found that objects, curves, function and sets are fractal when their form is extremely irregular and/or fragmented at all scales. Fractals are characterized by the fact that they show structures at all scales as shown in Fig-4. Such fragmentation at all scale indicates a scale dependence of various properties of fractals.
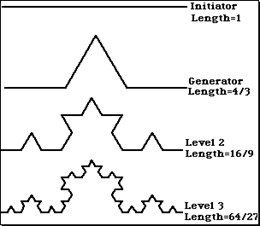
Fig-3successive approximation Koch curve DT =1, DF= ln4/ln3
Fig-4 -Zoom of fractal curve.
Fig-3 describes a typical Koch curve. The line-1 is called initiator. We then remove middle third of initiator replacing it by two lines each of length (1/3) as the remaining lines in each sides (2nd line in Fig-3). This is called the Generator which generates the new form. We repeat the process for level-2 and level-3. The length of the curve increases with each iterations. It has infinite length! The fractal dimension is found here to be DF =1.2628 (ln4/ln3) and length may be expressed as L(δ) = δ 1-D = δDT-DF where DF is fractal dimension and DT is topological dimension which is integer. One of the basic characteristics of fractal is geometry is its dependence on resolution.
Definition of Fractals:
An irregular geometric object with an infinite nesting of structure at all scales are defined as fractals. B. Mandelbrot, the father of fractal dimension has defined the fractals in several ways. He defined the fractal a set for which Housdorff- Besicovitch dimensions strictly exceeds the topological dimension. Another definition offered by him is as Fractal is a shape made of parts similar to the whole in some way which is termed as self similarity. An object is self-similar if it is congruent to a uniformly scaled piece of itself. Fractals are characterized by non differentiability and non integer dimensions. They are defined as sets of topological dimension DT and Fractal dimension DF such that DF> DT. Sometimes fractals are characterised by their scale divergence. This means that they are metric spaces for which a finite measure can be defined but whose standard measure which correspond their topological dimension like length of the curve, area of the surface etc. tends to infinite as resolution tends to zero. This includes power law divergences.
Similarly Fractal surfaces are characterized by surface fractal dimension greater than 2. Menger sponge is a 3d fractal but its fractal dimension is less than 3. Several kinds of fractals are defined. This includes usual fractal (power law divergence), underfractal (logarithmic divergence) and superfractal which shows exponential divergence. Usually fractal dimensions are non-integer but there are several kinds of fractals which has integer fractal dimension such as Brownian motion which has fractal dimension 2. However there are disagreement concerning the exact definition of fractal among mathematicians and it is suggested to use fractals without a pedantic definition.
Fractals-applications:
Fractals have wide range of application in almost every domain of science, engineering and bio sciences. There are lots of natural phenomena that can be defined and predicted using fractals. Some of these shapes include clouds, vegetables, colour patterns, lightning, and snowflakes. Fractal can define images that are not otherwise can be defined by Euclidean

geometry. Trees, rivers, coastlines, mountains, clouds, lightning, snowflakes and hurricanes, earthquake are all displaying or obeying fractal rules. A fractal description of many things is a story about how they grow. The fractal patterns are used by artists for a long time. The image created by a fractal is complex yet striking. Fractals are used to capture the complex organic structure and to analyze various biological processes or phenomena such as the growth pattern of bacteria. In lungs and blood vessels fractal structure can be observed with larger passages branching into smaller passages which branch again into yet smaller ones. It is widely used in image processing. Fractals are related to chaos as they are complex systems that have definite properties. Many disordered media are fractal structures. A number of works are done on deterministic fractal lattices by investigating random walk on them. It has been used to study the scattering of electromagnetic wave or scalar wave by random variation of refractive index. One of the interesting areas is the study of physics underlying irreversible growth phenomena that generates fractal structures or Kinetic Critical phenomena. New research has discovered that fractals can be put to good use in photonics by creating transparent ultrathin metallic electrodes with superior optoelectronic properties. Our world is fractal world. Its uses ranges from the branching of tracheal tubes, leaves, trees, vegetables, veins in hand, water swirling and twisting out of a tap, a puffy cumulus cloud, turbulent flow, tiny oxygen molecule or the DNA molecule and finally film and stoke market too!! There are many surprises in generating fractals and investigating their properties. It proves to be a useful tool despite all its intricacies.
A new approach to microphysics started with Fractals. The particle distribution in High Energy collision often show self similarity and power law behaviour which in turn can be related to the fractal structure of hadrons. Many works focuses on the path of the quantum particles and fundamental physics. The internal fractal structure of the path of quantum particle may be attributed to the non-differentiable space –time. In that respect laws nature can be replaced by scale relativity. This generalizes Einstein’s principle of (motion) relativity to scale transformation. Fractal is deeply related to in-homogeneity. Fractal approach has been made to study large scale distribution of galaxies which is a new approach for understanding galaxy clustering. Universe is suggested to have fractal structure at all scales. Fractals seem to prevail in nature starting from macro to micro scale. In the end if we ask why fractals? Possible answer could be structural manifestation of the fundamental non differentiability of Nature which leads to the fact that Laws of Nature are non-differentiable!!
References:
- Feder : Fractals, Plenum Press, (1989)
- B. Mandelbrot: Fractal Geometry of Nature, W.H Freeman and Co (1982).
- Nottale: Scale Relativity and Fractal Space Time. Imperial College Press (2011)
Pictures; Courtesy Google picture.
Visited 2616 times, 6 Visits today



